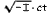 in place of t, as time-variable. If, in accordance with this, we insert
in place of t, as time-variable. If, in accordance with this, we insert
Albert Einstein: Relativity
Appendix
We can characterise the Lorentz transformation still more simply if we introduce the imaginary
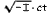 in place of t, as time-variable. If, in accordance with this, we insert
in place of t, as time-variable. If, in accordance with this, we insert
x1 = x
x2 = y
x3 = z
x4 = 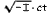
and similarly for the accented system K1, then the condition which is identically satisfied by the transformation can be expressed thus:
x1'2 + x2'2 + x3'2 + x4'2 = x12 + x22 + x32 + x42 (12).
That is, by the afore-mentioned choice of "coordinates," (11a) [see the end of Appendix II] is transformed into this equation.
We see from (12) that the imaginary time co-ordinate x4, enters into the condition of transformation in exactly the same way as the space co-ordinates x1, x2, x3. It is due to this fact that, according to the theory of relativity, the "time" x4, enters into natural laws in the same form as the space co ordinates x1, x2, x3.
A four-dimensional continuum described by the "co-ordinates" x1, x2, x3, x4, was called "world" by Minkowski, who also termed a point-event a "world-point." From a "happening" in three-dimensional space, physics becomes, as it were, an "existence" in the four-dimensional "world."
This four-dimensional "world" bears a close similarity to the three-dimensional "space" of (Euclidean) analytical geometry. If we introduce into the latter a new Cartesian co-ordinate system (x'1, x'2, x'3) with the same origin, then x'1, x'2, x'3, are linear homogeneous functions of x1, x2, x3 which identically satisfy the equation
x'12 + x'22 + x'32 = x12 + x22 + x32
The analogy with (12) is a complete one. We can regard Minkowski's "world" in a formal manner as a four-dimensional Euclidean space (with an imaginary time coordinate); the Lorentz transformation corresponds to a "rotation" of the co-ordinate system in the four-dimensional "world."
Next: The Experimental Confirmation of the General Theory of Relativity