Works of Lev Vygotsky
Primitive man’s numerical operations provide the best illustration of the development of his thinking and its dependence on the enhancement of the external signs on which it relies. Many primitive peoples do not count beyond 2 or 3.
We should not conclude from this, however, that they are incapable of counting above three. It simply means that they lack abstract concepts, extending beyond those numbers. They are incapable of using operations that are inherent in our mode of thinking, yet, as LÚvy-Bruhl has observed, “up to a point they are able, by means of operations which are peculiarly their own, to reach the same results.”
These operations rely more heavily on memory. Primitive man counts differently from us – for the most part by concrete means; and in this concrete counting mode he again surpasses civilized man. In other words, research into the processes of counting in primitive man has shown that in this respect, as with memory and speech, primitive man is both poorer and, at the same time, richer than civilized man. It would therefore be more correct here,. to speak not of a quantitative difference, but of a qualitatively different mode of counting in primitive man.
If we were to attempt a concise description of the counting processes used by primitive man we would have to say that its dominant feature is the development of his natural arithmetic. He counts by means of concrete perception, natural memorization and comparison, without resorting to the technical operations devised by civilized man as aides to counting. Since we count exclusively with numbers, We are inclined to believe that anyone lacking numbers higher than three is unable to count above three. LÚvy-Bruhl argues as follows: “Does it make sense for us to claim that the same results cannot be achieved in any other way? Is it really out of the question for the primitive mind to have its own operations and its own special processes in order to achieve the same goals that we achieve with our numerical system?” Primitive man perceives a group of objects from a quantitative point of view. In this case, the quantitative sign acts as a directly perceived quality, distinguishing that group from other groups. Primitive man can judge externally as to whether it is complete.
It should be noted that direct perception of quantities can also be found in civilized man, mainly where ordered quantities are concerned. If a musician were to omit a single measure in a piece of music, or if someone reading a poem were to omit a single syllable, we would immediately conclude, without resort to counting, and on the basis of our direct perception of the rhythm, that one measure or one syllable was missing. It was for this reason that Leibnitz called music “unconscious arithmetic.”
Something similar occurs with primitive man when he perceives groups consisting of different numbers of objects. The difference, for example, between 12 apples and 3 apples is evident from an immediate impression. The difference between these two quantities may be perceived concretely, with no need for any counting. We do not find this surprising; in this respect we possess the same ability to tell at a glance which is the bigger group of objects.
What researchers have usually found astonishing is the subtle differentiation of which primitive man is capable in this art. They report that primitive man, relying on an exceptional memory, has enhanced this direct perception to a very high degree. He is capable, by comparing current impressions with the image stored in his memory, of telling whether a single object is missing in any larger group.
Dobrizhoffer finds that “primitive man not only does not know arithmetic, he avoids it. His memory proves to be a major handicap; counting bores him, so he is unwilling to use it. “When members of a primitive tribe return from an expedition hunting from wild horses, nobody asks how many wild horses they have brought back. The question asked is, “How large an area would the herd you brought back occupy?”
When a primitive tribe is about to set out on a hunting trip they glance over their many dogs, and tell instantly if one is missing. Primitive man is similarly able to notice the absence of a single head of livestock from a herd of several hundred. Such precise differentiation is essentially a further development of the same direct perception of quantities that we find in ourselves.
While distinguishing a group of 12 apples from a group of 3 is as easy as distinguishing red from blue, telling the difference between a herd of 100 head of livestock from one with 101 is a difficult as telling the difference between two blues, one a shade darker than the other. Fundamentally, however, it is the same operation, raised by practice to a higher level of differentiation.
It is interesting to note that contemporary civilized man also has to revert to this concrete visual perception whenever he seeks a clear visual sense of the difference between two quantities. Wertheimer is right to argue that the natural arithmetic of primitive peoples, like their entire mode of thinking, yields results that are both higher and lower than ours. Lower, because certain operations are entirely beyond the reach of primitive man, and his capabilities in this regard are severely limited. Higher, because his thinking is permanently rooted in reality; lacking abstraction it directly renders the live concrete situation. As we ourselves find in everyday life and in art, such concrete images prove much more true-to-life than abstract representations.
When a modern pacifist wants to convey a compelling idea of the number of people killed in a war, to drive his point home he translates the abstract arithmetical total into new concrete, though artificial terms. He might say that if the bodies of those killed in the war were laid out shoulder to shoulder they would stretch all the say from Vladivostok to Paris. By means of such vivid imagery he hopes to convey an immediate sense of the colossal number of lives lost, as in a visual perception.
Similarly, when we use a conventional diagram to represent the simplest thing, such as the respective consumption of soap in China and Germany, we might draw the figure of an enormous Chinaman and a much smaller German, symbolizing how much more populous China is than Germany; beneath them we might draw two pieces of soap, one tiny and the other enormous, so that the entire picture and the diagram create a greater impact than mere abstract arithmetical data. It is precisely this kind of picture and graphic device that figures prominently in the natural arithmetic of primitive man.
LÚvy-Bruhl notes that primitive man regards our numbers as unnecessary and is incapable of using them. For him numbers are quite irrelevant to the large quantities he is able to count in quite a different way.
This concrete or figurative aspect of primitive counting manifests itself in a number of special traits. According to Thurnwald, if primitive man wishes to refer to a small group of people, he does not name the total number, but says the name of each one known to him personally; those whose name he does not know he enumerates on the basis of some other concrete feature, for example, the man with the big nose, the old man, the child and the man with the skin disease – all in order to say that four people have arrived.
A large number is initially perceived as the image of some kind of picture the image and the quantity merging into a single set. That is why, as we have seen, the primitive mind is incapable of abstract counting, being capable of counting only as long as the process of counting seems linked to reality. Among the primitive peoples, therefore, numerals are always names designating something concrete – a numeral image or form used as a symbol for a certain quantity. Very often these are simply auxiliary devices of memory.
The decisive factor, however, is not this, but the direction taken by the development of counting in primitive man, which proceeds not via the enhancement of natural arithmetic, but along exactly the same lines as the development of memory and thinking in primitive man – the creation of special signs whereby natural arithmetic is transformed into civilized arithmetic.
Admittedly, among the primitive peoples even this use of signs is still purely concrete and visual. The simplest method used by primitive man for counting is a comparison between the parts of the body and various groups of objects. At his highest level of development, therefore, he not only glances at such groups, but is already making a quantitative comparison between them and another group, such as his own five fingers. In a single, quantitative respect he compares a group of objects that needs to be counted with some kind of counting tool.
Primitive man thereby makes a major step towards abstraction, and a major transition to completely new paths of development. Yet his use of this new tool, to begin with, remains purely concrete. Even here primitives count in a purely visual manner. They touch all their fingers, and parts of their hands, shoulders. eyes, nose, forehead in succession, and then all those same areas again from the other side, thus equating by purely visual means the number of objects to the parts of the body, as counted in a certain order.
There are still no real numerals in such a process. As LÚvy-Bruhl has pointed out, this is a concrete operation of memory designed to define a certain plurality. Haddon sees this system as an auxiliary counting tool. It is used in the same way as the string with knots, and not at all as a series of true numbers. It is a mnemonic device. rather than a numerical operation. Here there are no that in such a method of counting, the same word may designate different quantities: for example, in New Guinea, the word ano (neck) means both tens and fourteen.
Similarly, among other peoples, the words for finger, shoulder and hand mean different quantities, depending on whether they are used in counting on the left or the right side of the body. The same author concludes that these words certainly do not stand for numbers. He poses the following question: “How could the same word, doro, stand for 2, 3 and 4 as well as 19, 20 and 21, unless it were so defined by a simultaneous gesture involving one of three fingers on the right hand, or one of the corresponding fingers on the left hand?”
Brooke quotes a remarkable instance in which a native of Borneo tried to remember his instructions. He was required to visit forty-five formerly rebellious but now subdued villages and tell them the amount of the fines they had to pay. How did he go about it? He produced several dry leaves, which he divided into pieces. His supervisor replaced them with paper. He laid these out, one at a time, on the table, while counting them on the fingers of both hands. He placed his foot on the table, and then began counting, on his toes, more pieces of paper, each of which stood for the name of a village, the name of its chief, the number of its warriors and the amount of the fine. Having exhausted his toes, he went back to his fingers. When he had finished counting, there were 45 pieces of paper laid out on the table.
He asked to have his instructions repeated. While this was being done, he ran his hands along his pieces of paper and counted on his fingers and toes, as before. “This is how we write”, he said; “you white people cannot read like us.” Late in the evening he repeated everything accurately, putting a finger on each separate piece of paper. He said, “If I can remember all this tomorrow morning, everything will be fine, we will leave these bits of paper on the table.” He then piled them all up at random. Next morning he laid out the pieces of paper in exactly the same order as the day before, and repeated all the details, with complete accuracy. Throughout the month he spend going from one village to the next, far in the hinterland, he did not forget one of these different amounts.”
“The act of arranging pieces of paper”, as LÚvy-Bruhl remarks “instead of the hands or toes, is particularly remarkable. It provides us with an absolutely pure example of the ‘concrete abstraction’ inherent in prelogical thinking, that has lost none of its original concreteness.” It is truly hard to image a more striking example of the most essential difference between human and animal memorization. When confronted with a task beyond his abilities, primitive man resorts to paper, fingers and the creation of external symbols.
He tries to act upon his memory from the outside. He organizes the internal processes of memorization from the outside, supplanting internal operations by external activity over which he has more control. By organizing this external activity he dominates his memory with the aid of symbols. Therein lies the essential difference between human and animal memory. At the same time, this example also shows how closely operations of counting are associated, in primitive man, with those of memory.
Roth asked one primitive how many fingers and toes he had, and invited him to mark their number with lines in the sand. He began to bend two fingers on each hand and for each pair drew a double line in the sand. A similar method is used by tribal chieftains for counting people. We interpret this as an indirect instrumental way of formulating a representation of quantity with the aid of symbols. As we can see, the transition from natural arithmetic, based on the direct perception of quantities, to a mediate operation performed with the aid of symbols, is already situated at the first stages of the cultural development of man.
Such counting, using the parts of the body, and such concrete numeration, which gradually becomes semi-abstract and semi-concrete, forms the first phase of our arithmetic. Haddon writes, “One cannot say that nagibet is the name of the number five. It merely means that there are as many objects as there are fingers on one hand!’ Such counting is therefore based on a tacit graphic of pictorial comparison, a manual or – as this author puts it, a visual-concept, without which the development of primitive numerical operations would be incomprehensible.
This graphic origin of numerical terms is also made evident by the fact that primitives tend to count not in ones, but in the most diverse groups, in twos, fours, fives and so on. This is why, though they often have at their disposal only the very few numerals to which that group is limited, they can still count very large numbers, by the repeated use of the, same numerals.
The concrete nature of this process is further illustrated by the existence, among primitive tribes, of different systems of counting, for example, flat or round objects, animals and people, time, long objects, etc. Different objects must be counted differently. The Mikir language, for example, has separate counting systems for people, animals, trees, houses, flat and round objects and parts of the body. The numeral is always the number of a given object.
Vestiges of this survive in the counting methods we apply to different objects. To this day, for example, we count pencils in dozens and gross, etc. In this respect, the auxiliary words used by many primitive peoples when counting are of particular interest. Their function is, as it were, to help people visualize the subsequent stages of the arithmetical operation. In such a language, for example, “twenty-one pieces of fruit” sounds literally as follows: “Over twenty pieces of fruit I place one on the very top!’ “Twenty-six pieces of fruit” will sound like “Over two groups each of ten pieces of fruit I place six on top.”
Here, as noted by Levy-Bruhl, we see in arithmetic that same graphic quality that we have found in the general structure of primitive language. Paradoxically, he notes, one has to conclude that in the lower societies man counted for many centuries without any numbers at all. It would be wrong to argue that the human mind constructed numbers in order to count, because in actual fact people began to count before they had succeeded in creating numbers.
Wertheimer provides a sound explanation of the link between the numerical operation and concrete situations, by showing that the numerical images used by primitives are focussed on real possibilities. Whatever they find impossible in real life is also impossible for them in their counting operations. Wherever there is no live concrete connection between things, there is also no logical relationship for them. From the standpoint of primitive man, for example, 1 horse + 1 horse = 2 horses; 1 man + 1 man = 2 men; 1 horse + 1 man = 1 horseman.
Wertheimer has raised the general question of how these people behave when confronted with such mental tasks, in real life situations where we would use numbers. It appears that primitive man is very frequently obliged to cope with such situations. In so doing he operates at the lowest levels of his development, by means of direct perceptions of quantity, but at the highest levels by means of numerical images which are used as symbols or tools, while still retaining their purely concrete nature.
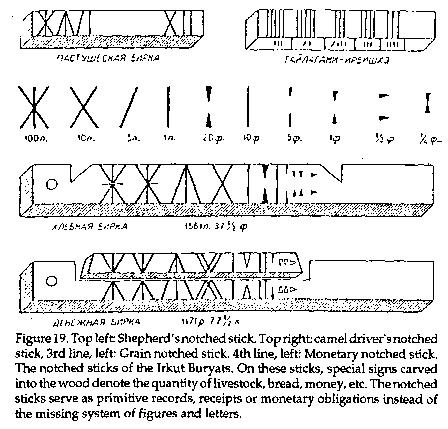
The symbols or auxiliary tools at the early stage include pebbles, fingers and sticks, which later developed into notched sticks (Figure 19). Eventually, when the primitive runs out of fingers for counting, he will count on the fingers of a friend, inviting, if necessary, a third person, it being understood that the fingers of each new person stand for a new series of ten.

In the counting systems employed by primitive peoples, we often come across signs resembling those in the Roman system. The Zunis, for example, use knots to designate all numbers: a simple knot stands for one, a more complex knot, five; and an even more complex one, ten. Two means one plus one. Five with the preceding simple knot means four; five with the next knot means six. This system for denoting a lower quantity by deducting one from a higher quantity suggests that primitive man is arithmetically inclined towards rounded and completed natural groups (fingers, etc).
One researcher reports a remarkable instance of primitive counting, which illustrates the development of numerical systems. Primitives first count on the fingers of one hand, while saying out loud as they go, “that’s one”, etc. When they get to the last finger, they add: “one hand”. They then count the fingers of the other hand in the same way, and then their toes. If they have not finished counting, they thereafter count “one hand” as a unit of a higher order. Now, when counting on fingers and toes, each one counts as five, or as whole hand.
Psychologists have induced this operation in a purely experimental manner. Let us suppose that we invite any group of civilized people to count 27 objects, warning them at the same time that for the purposes of the exercise they, like certain primitive peoples, do not know how to count higher than five. As our experiments have shown, some members of the group cannot solve the problem at all; some others solve it by departing from the rules; while the rest solve it perfectly correctly, and each in an entirely identical fashion.
‘They count up the objects, repeating all the time the series from one to five; then they count up the fives and express the result as follows: five fives plus two. Research has shown that our decimal counting system is also based precisely on this device. It is always like counting on two threads; we count the objects themselves, and then count our count, or the groups of those objects. When I count 21, 22, 23 ... and then 31, 32, 33, I am actually relying solely on the 1, 2, 3 for the purpose of counting, whereas the word “twenty” and “thirty”, which is added each time, tells me that I am counting within the second range of tens.
Experimental research has led to the extremely interesting conclusion that our counting system does the counting for us. Whereas primitive man is obliged to divide his attention, by first counting single objects on his fingers, and then, on those same fingers, the total number of hands, our decimal system itself performs that same function on our behalf. Psychologists argue, for this reason, that from a psychological standpoint, when we count we are really recalling, rather than counting. We automatically use our numerical system, reproduce a numerical series in order, and, on reaching a certain point, recognize the ready result. What we see in a hidden, automated and already developed form in adult civilized man, also occurs in primitive man, but still in a visible form that is in the process of development.
It is interesting to note that such specific aids are used not only in simple counting, but also in some rather complicated arithmetical operations. Wertheimer describes a remarkable method of computation, which was found among the Kurds along the Russo-Persian border. As they still lack an abstract counting operation, the Kurds multiply in the following manner: figures from 6 to 10 are designated by bending one, two, three or five fingers (meaning, of course. plus five). Multiplication from 5 x 5 to 10 x 10 is done in such a way that bent figures are interpreted as tens, and straight fingers are multiplied as units.
For example, let us multiply 7 x 8. On one hand, two fingers are bent (2+5=7); and on the other, three (3+5=8); the hands are joined; the bent fingers are added (2+3=5), and the straight fingers are multiplied (2x3=6). Result: 56.
Leroi has observed that among the civilized peoples it is possible to find numerical pluralities or images (century, year, week, month, squadron are all numerical images). He inquires, “What makes the Fijian word kogo, meaning a hundred coconuts, more primitive than the word century, meaning a hundred years?” In our society, ten soldiers walking separately are ten men; but when in formation with a corporal, they become a platoon. In the example, Leroi sees a parallel with the fact that in primitive languages numbers “describe special circumstances” and accounts.
His main conclusion seems irrefutable: the numeration of primitives cannot be compared with the “numeration” of animals: in other words, the whole of primitive arithmetic must not be treated as the mere direct perception of quantities. Whenever it seeks to cross certain boundaries, this embryonic numeration has to resort to the aid of concrete mnemotechnics (the use of fingers or sticks): in fact this combination of natural arithmetic (the direct perception of quantities) and mnemotechnics is the most essential feature of primitive numeration. Leroi rightly compares this arithmetic with the counting of the illiterate and the use of visual numbers (diagrams) in our society.
The further development of “civilized mathematics” is very closely linked to the evolution of signs and the ways of using them. This applies not only to the lower, but also to the highest levels of the development of scientific mathematics. When explaining the substance of the algebraic method, Newton said that in order to solve questions related to numbers or abstract relations between magnitudes, one has simply to translate the problem from English or another language in which it is proposed into algebraic language, which is capable of expressing our concepts about the relations between magnitudes.
Sheremetyevsky, in his study entitled “History of Mathematics”, thoroughly illustrates the role of symbols as tools. “As for mathematical analysis itself, it has one characteristic which makes it a genuine thinking machine, working with the speed and accuracy one expects from a well-tuned mechanism. I refer to the device of the symbolic recording, by means of algebraic signs, of all the conclusions of analysis.”
Comparing contemporary algebra, which uses these signs, and the rhetoritical algebra of the ancients, he concludes that the entire psychological effort devoted to the solution of problems assumed a new structure under the impact of the new technique for designating operations. Referring to the mathematicians of antiquity, he writes, ‘They were deprived of the symbolism that serves to mechanize reasoning, and from which modern algebra derives its immense superiority. In their unsymbolized or rhetorical algebra, memory and imagination had to be exercised intensively in order to retain a constant grasp of all the logical threads connecting the ultimate conclusions and the terms of the problem. Ancient mathematicians had to develop that very special type of mind set one finds in chess players who do not look at the board during a game. The fact that Euclid gave rise to no imitators, and that the theory of incommensurables remained unchanged for 1,800 years conveys some idea of the superhuman powers of abstract reasoning that were required for this kind of work.