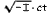 , by x1, x2, x3, x4, we also obtaill the result that
, by x1, x2, x3, x4, we also obtaill the result that
Albert Einstein: Relativity
Part II: The General Theory of Relativity
We are now in a position to formulate more exactly the idea of Minkowski, which was only vaguely indicated in Section 17. In accordance with the special theory of relativity, certain co-ordinate systems are given preference for the description of the four-dimensional, space-time continuum. We called these " Galileian co-ordinate systems." For these systems, the four co-ordinates x, y, z, t, which determine an event or — in other words, a point of the four-dimensional continuum — are defined physically in a simple manner, as set forth in detail in the first part of this book. For the transition from one Galileian system to another, which is moving uniformly with reference to the first, the equations of the Lorentz transformation are valid. These last form the basis for the derivation of deductions from the special theory of relativity, and in themselves they are nothing more than the expression of the universal validity of the law of transmission of light for all Galileian systems of reference.
Minkowski found that the Lorentz transformations satisfy the following simple conditions. Let us consider two neighbouring events, the relative position of which in the four-dimensional continuum is given with respect to a Galileian reference-body K by the space co-ordinate differences dx, dy, dz and the time-difference dt. With reference to a second Galileian system we shall suppose that the corresponding differences for these two events are dx1, dy1, dz1, dt1. Then these magnitudes always fulfil the condition 1)
dx2 + dy2 + dz2 - c2dt2 = dx1 2 + dy1 2 + dz1 2 - c2dt1 2.
The validity of the Lorentz transformation follows from this condition. We can express this as follows: The magnitude
ds2 = dx2 + dy2 + dz2 - c2dt2,
which belongs to two adjacent points of the four-dimensional space-time continuum, has the same value for all selected (Galileian) reference-bodies. If we replace x, y, z, 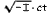 , by x1, x2, x3, x4, we also obtaill the result that
, by x1, x2, x3, x4, we also obtaill the result that
ds2 = dx12 + dx22 + dx32 + dx42
is independent of the choice of the body of reference. We call the magnitude ds the " distance " apart of the two events or four-dimensional points.
Thus, if we choose as time-variable the imaginary
variable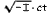 instead of the real quantity t, we can
regard the space-time contintium — accordance with
the special theory of relativity — as a "Euclidean"
four-dimensional continuum, a result which follows
from the considerations of the preceding section.
instead of the real quantity t, we can
regard the space-time contintium — accordance with
the special theory of relativity — as a "Euclidean"
four-dimensional continuum, a result which follows
from the considerations of the preceding section.
Next: The Space-Time Continuum of the General Theory of Realtiivty is Not a Euclidean Continuum
1) Cf. Appendixes I and 2. The relations which are derived there for the co-ordlnates themselves are valid also for co-ordinate differences, and thus also for co-ordinate differentials (indefinitely small differences).