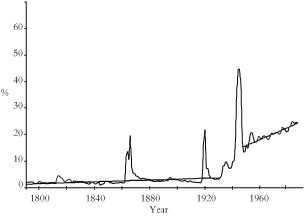
Figure 1: Ratio of total government tax revenue to GDP across 21 developed countries (percentage) [36]
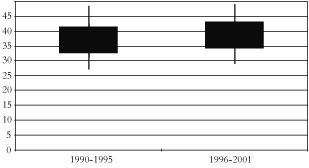
Figure 2: US state spending as a proportion of GNP
From International Socialism 2 : 117, Winter 2008.
Copyright © International Socialism.
Downloaded with thanks from the International Socialism Website.
Marked up by Einde O’Callaghan for the Marxists’ Internet Archive.
A new word [1] entered the vocabulary of the left in November 1999 with the momentous protest against the World Trade Organisation in Seattle – ”neoliberalism”. [2] Just as the movement that erupted at that protest defined itself as being against “globalisation” (or “corporate globalisation”), so it came to describe itself as “anti-neoliberal”. The far left took over this terminology, often describing economic policies it opposed as “neoliberal”.
But there was an ambiguity in the term “neoliberal”. Did it refer to a way of running the capitalist system that could be changed with a change in government policy, or did it refer to something intrinsic to the present phase of capitalism that only challenging the system as whole could overcome? And was this present phase really described by the right wing “libertarian” anti-statist ideology of the neoliberals or was it a much more complex system of attacks?
Many of the most influential thinkers in the post-Seattle movement accepted the first answer to both questions. Leaders of Attac in France said their organisation was not “anti-capitalist”, but merely wanted to stop short term financial flows disrupting national economies. [3] Bernard Cassen, founder of Attac, wanted a “protectionist” national economy organised along capitalist lines. Susan George would occasionally speak about capitalism, but could also write of “the harmful consequences of globalisation”, as if this were something separate from, and intrinsically worse than, capitalism.
When it came to explaining what had changed since the 1960s, the emphasis tended to be on the victory of one ideology over another, rather than changes in the inner functioning of the global economic system. This was put very clearly by the French sociologist Pierre Bourdieu. He argued, “The main issue is neoliberalism and the retreat of the state. In France neoliberal philosophy has become embedded in all the social practices and policies of the state”. [4] This was “the effect of a shared belief ... which has created a climate favourable to the withdrawal of the state and so submission to the values of the economy”. [5]
The logic of this position was that all that was needed to reverse the unpleasant policies pursued by capitalist governments and corporations was a shift in ideology or politics at the top of society. Pressing for this could involve alliances with particular capitalist groups. Susan George spelt this out in theory, writing that “sometimes the allies may even be ... transnationals” such as those in the insurance industry. [6] Bernard Cassen applied this in practice by giving electoral support to the former French defence minister Jean-Pierre Chevènement.
Such approaches contrasted sharply with the analyses of those of us who saw the faults falling under the rubric “neoliberalism” as flowing from the logic of capitalism at a certain stage in its development. This did not prevent us joining with the wider movement in agitating against those faults. As I wrote at the time, “Hundreds of thousands, perhaps millions of people are beginning, for the first time, to challenge the global system. They come from a vast range of backgrounds and experiences, and bring with them the differing ideas that have developed there”. [7] The different approaches were, however, bound to work themselves out in practice at some point. I added, “The movement will not be able to develop beyond a certain point unless such arguments are resolved”. [8]
Developments over the past two years show that the arguments are indeed becoming important in practice. Alex Callinicos and Chris Nineham have written about the debilitating divisions that emerged in the World Social Forum movement that arose out of Seattle [9], while Daniel Bensaïd and Pierre Rousset have pointed out:
The “pillars” of the alterglobalisation – the Brazilian Workers Party and Rifondazione Comunista – lead or actively participate in centre-left governments, implementing openly social liberal policies. This evolution in less than six years is full of consequences. The problem does not lie in the suddenness of the conversions ... The lack of resistance that they have encountered within their own parties must focus attention both on the limits of the anti-neoliberal rhetoric and the profound resignation that it has partially masked. [10]
For this reason it is necessary to take up once again the analysis of the relationship of neoliberalism to capitalism – and by implication, of anti-neoliberalism to anti-capitalism. [11]
A number of Marxist analyses have attempted to come to terms with neoliberalism, for instance Gerard Duménil and Dominique Lévy’s Capitalism Resurgent, François Chesnais’s La Mondialisation du Capital and, probably most influentially, David Harvey’s The New Imperialism and A Brief History of Neoliberalism.
These works contain a mass of useful information about the world today. But they are also marked by the same ambiguity over neoliberalism to be found in the non-Marxist writings within the movement. All make reference to the problems faced by capitalism in the 1970s that led to a new period of crises. But they suggest that it is not capitalism as such that is to blame; rather it is a particular regime of capitalism. So Duménil and Lévy say that the new period was heralded by a fall in the rate of profit from which the system has not yet fully recovered, [12] but then go on to describe the advance of neoliberalism as a “coup” (no less) by “finance capital” in the late 1970s. [13] This coup supposedly overturned the “Keynesian” approach of industrial capital, which had been based on accumulation through a “compromise” with working class organisations on the terrain of the welfare state. [14]
Chesnais’s tone is often similar. He also refers to a “coup d’etat” in the late 1970s. He writes that “industrial capital” has been forced to subordinate itself to “money capital”. [15] Chesnais is a revolutionary socialist, but the implication of his argument is that, if “industrial capital” still dominated “finance capital”, capitalism today would not be experiencing a “mediocre or poor dynamic of investment” or “the destruction of industrial employment ... and strong pressures which weigh on those jobs which remain”. [16]
Essentially the same arguments are to be found in David Harvey’s work. He presents a picture of capitalism in the US, Western Europe and Japan before the mid-1970s expanding on the basis of “a class compromise between capital and labour”. This meant an acceptance that:
The state could focus on full employment, economic growth and the welfare of its citizens, and that state power should be freely deployed alongside of, or if necessary, intervening in or substituting for market processes to achieve these ends. Fiscal or monetary policies usually dubbed “Keynesian” were widely deployed to dampen business cycles and to ensure reasonably full employment. [17]
He calls this “embedded liberalism” and argues that it “delivered high rates of economic growth in the advanced capitalist countries in the 1950s and 1960s” and that a “social and moral economy was fostered through the activities of an interventionist state”. [18]
He recognises that this system broke down in the mid-1970s. This was, he argues, caused by “a crisis of over-accumulation”, which he sees as persisting into the present. [19] But he goes on to imply, again and again, that an alternative was possible within the existing system.
Capitalists, he argues, adopted the neoliberal approach because their class power had been diluted under Keynesianism and was threatened in the mid-1970s. Their response was determined by their need for a “restoration of class power” [20] – or even because “neoliberalism creates conditions for class formation”. [21]
One particular expression of this reassertion of class power has been the domination of finance over industry: “There was undoubtedly a power shift away from production to the world of finance ... In a conflict between Main Street and Wall Street, the latter was to be favoured.” Harvey continues, “One substantial core of rising class power under neoliberalism lies, therefore, with the CEOs, the key operators on corporate boards, and the leaders of the financial, legal and technical apparatuses that surround this inner sanctum of capitalist activity.” And while they rise in power, the unfortunate shareholders are among those who suffer: “The power of the actual owners of capital, the stockholders, has been somewhat diminished”. [22]
From this it follows not simply that there is an alternative within capitalism, but also that this alternative might actually be more favourable to capitalism: “Paradoxically, a strong and powerful social democratic and working class movement is in a better position to redeem capitalism than is capitalist class power.” This, he writes, might “sound a counter-revolutionary conclusion” but “it is ordinary people who suffer, starve, and even die in the course of capitalist crises rather than the upper classes”. [23]
In The New Imperialism Harvey suggests how a reformed capitalism might work:
The United States could downgrade if not turn away from its imperialist trajectory by engaging in a massive redistribution of wealth within its borders and redirection of capital flows into the production and renewal of physical and social infrastructures ... A massive counterattack within the US as well as in the other core countries of capitalism against the politics of neoliberalism and the cutting of state and social expenditures might be one of the only ways to protect capitalism internally from its self-destructive and crisis prone tendencies. [24]
A very similar approach is to be found in Duménil and Lévy, who argue that the “Keynesian view of the history of capitalism, including its current problems ... is very sensible” and “one can only regret that the political conditions of recent decades have not made it possible to stop the neoliberal offensive and put to work alternative policies ... in the context of other social alliances”. [25] The logic of this argument is that left wing socialists might be justified in joining centre-left governments such as those in Brazil and Italy. Compromising on anti-capitalism can, it would seem, permit a challenge to neoliberalism.
What is the real character of neoliberalism? The question is not as easy to answer as it might seem.
At one level neoliberalism is an ideology. Literally “neoliberalism” means the “new liberalism”, and “liberalism” in its continental European (as opposed to North American) sense means “free market economics”. As such it is a resurrection of the orthodox “laissez faire” economic ideology that prevailed until the great slump of the 1930s. This ideology contended that free market economies will run smoothly, steadily producing more wealth. Any problems that arise are supposedly a result of “unnatural monopolies” (especially in the labour market), which prevent the free movement of prices and wages pulling supply and demand together. State intervention is seen as distorting the economy and has to be restricted to defending private property, national defence and, in the monetarist version of neoliberalism, overseeing the money supply. The ideology is backed by supposed rigorous “neoclassical” economic theory, which purports to show mathematically that free markets always “clear” – that is, all labour will be employed producing goods that are all sold. [26]
Economic “liberalism” of the old sort fell into disrepute as an ideology by the end of the Second World War. In fact, it had already begun to be superseded as a practice by the beginning of the 20th century, when, as Rudolf Hilferding, Nikolai Bukharin and Lenin pointed out, “free market capitalism” began to give way to monopoly capitalism and its product, imperialism. State intervention was seen as necessary to provide the infrastructure for capitalist production (railways had long been nationalised in Germany, and in Britain conservative governments nationalised the electricity grid and the airlines). The subsequent organisation of the national economy for war, first in Germany and Japan, then in Britain and the US, showed that state intervention could provide a basis for renewed profitability and accumulation.
It was against this background that a new orthodoxy emerged, preaching state intervention as the way to protect capitalism against itself. The new orthodoxy based itself on the ideas of the British economist John Maynard Keynes, who in the 1930s partially revised the neoclassical ideas he had previously backed wholeheartedly. [27] As Al Campbell has noted, after the Second World War “capital adopted Keynesian ideas because it believed that the various restric-tions and regulations would be beneficial to the process of capital accumulation at that historical moment, particularly in comparison with the poor record of accumulation presented by its recent experience without those restrictions during the Great Depression”. [28]
There was always some resistance to the new Keynesian orthodoxy. A minority of economists, notably Friedrich von Hayek and Milton Friedman, continued to hold on to the old doctrine. Campbell claims that “most finance capital never accepted the Keynesian compromise”, but that it accounted for only 15 percent of capital. [29] Governments and big corporations accepted Keynesian ideology, not because it was imposed upon them by working class strength, but because increased economic activity by the state was accompanied by much higher levels of profitability in the US and major European states than under the pre-war ideology of economic liberalism.
Keynesianism as an ideology reflected the reality of capitalism in the period after the Second World War. National economies were increasingly dominated by near-monopolies that worked with the state to struggle for global dominance against near-monopolies based in other national economies. The result was a seemingly relentless trend towards increased state involvement in capitalist accumulation that had begun in the 1880s. To those of us who were taught economics in the early 1960s, Keynesianism was the explanation for the sustained economic growth of the post-war years. Yet as Robin Matthews pointed out long ago, the economic expansion of post-war Britain did not depend on Keynesian “remedies” for recurrent crises or on higher levels of government investment than in the pre-war years. [30]
An important by-product of the statified capitalist economy (and of its arms spending in particular) in the industrially advanced countries was full employment and therefore a degree of working class strength, which, in the late 1950s and 1960s, capital had to make concessions to. But to see these concessions as causing the statification or the long boom is to get things completely the wrong way round.
Keynesianism as an economic practice, rather than an ideology, was not put to the test until the first serious economic crisis in 40 years erupted in the mid-1970s – and it proved incapable of dealing with it. Capitalists were faced with a combination of recession and rising prices known as “stagflation”. The Keynesians were at a loss. As one, Francis Cripps, put it, they suddenly realised that “nobody really understands how the modern economy works. Nobody really knows why we had so much growth in the post-war world”. [31] Within three or four years Keynesianism had been replaced as the orthodoxy by reborn versions of the ideas it had pushed aside four decades earlier. This was not a question of states somehow coming to accept a wrong set of ideas:
There was a structural crisis of capitalism. That is, the policies, practices and institutions that had been serving well capitalism’s goal of capital accumulation ceased to do so. More narrowly, one can say that capitalism abandoned the Keynesian compromise in the face of a falling rate of profit, under the belief that neoliberalism could improve its profit and accumulation performance. [32]
In its first phase this rebirth of old ideas took the form of “monetarism”. Milton Friedman, the central figure in monetarism, claimed that any problems with the free market system were caused by governments’ inept control of the supply of money. But this version of free market economics proved unworkable in less than a decade, and the emphasis shifted to versions like those of von Hayek and Robert Lucas, which were even more critical of state intervention than Friedman’s. [33] The ideas were popular with supporters of capitalism for a number of reasons.
Partly there was simple apologetics. Powerful voices had emerged from the popular struggles of the late 1960s and early 1970s challenging the legitimacy of capitalism. The mainstream defence against such voices had been that Keynesian state intervention had proved capitalism could satisfy people’s needs. Now that claim fell apart in the face of economic crisis. The argument had to be turned upside down. State intervention was now presented as the problem rather than the solution.
This was especially pleasing for those who dealt in finance rather than production, because under the new orthodoxy any way of making money was necessarily beneficial. Neoliberalism saw sitting at home receiving interest or dividend payments as an incentive to production, and therefore a valuable social activity. As Nikolai Bukharin had pointed out long before, it was “the economic theory of the leisure class”. [34]
But more than apologetics was involved. There was a sense of desperation within capitalist circles in the mid-1970s. The first signs of crisis in their system coincided with growing assertiveness among workers. There had already been attempts to counter this in the late 1960s and early 1970s. Wage controls were imposed in Britain in 1966–70, 1971–2, 1973–4 and 1975–9; and in the US in 1971. Left wing supporters of Keynesianism tend to forget that these were an integral part of the post-war orthodoxy. But wage controls were not effective. They might work for a year or two, but they built up resentment among workers, which encouraged militancy even where it had hardly existed before, and they eventually fell apart amid waves of strikes.
The reborn free market approaches presented by Friedman and Hayek seemed to offer a way out. They claimed that the economy would resolve its own problems if it were freed from “distortions” to the market – whether these came from state intervention or from trade union interference with the “flexibility” of the labour market. Free trade would prevent national monopolies distorting prices, and unemployment would settle at the “natural rate” necessary to prevent wages eating into profits.
Ruling class ideologies are rarely just lies cynically spread in order to win the acquiescence of the ruled. They are sets of beliefs that give the ruling class a sense of its own importance, sanctify its rule in its own eyes as well as in the eyes of others and provide it with confidence that it can deal with any apparent flaws in its own system. Keynesianism fulfilled this role during the post-war decades in the advanced Western countries, as did Stalinism in the “Communist” states and “developmentalism” in Latin America, as well as the post-colonial states of Africa and Asia. But it became increasingly clear from the mid-1970s onwards that state intervention could not prevent economic crises in any of the world’s regions. [35] Neoliberalism succeeded in filling the ideological gap. As such it appealed not just to finance capital, but to productive capital as well.
It is important to differentiate between the claims of any ideology and what those who hold it actually do. There is rarely a direct correlation between the two. Yet many commentators, on the right and left alike, continue to make claims about neoliberalism that simply do not fit the empirical record of the past three decades.
First, there is the widespread belief that neoliberalism involves a retreat of the state. This is falsified by a glance at the rate of state expenditure in the advanced capitalist countries.
|
Figure 1: Ratio of total government tax revenue to GDP across 21 developed countries (percentage) [36] |

|
|
Figure 2: US state spending as a proportion of GNP |

|
As I have pointed out before in this journal, multinational corporations continue to be rooted in states. [37] The biggest have half their assets, markets and labour forces located in a single home state, to which they look to protect their interests. Capitalism can no more do without the state today than it could in the Keynesian period. State intervention has been used to drive through attacks on workers, as with Margaret Thatcher’s anti-union laws or the use of the police against the miners’ strike of 1984-5. But it has also repeatedly been used to protect sections of capital against the effects of crisis in a way supposedly ruled out by neoliberal ideology. The US state helped bail out Chrysler when it came close to going bust in 1979; it took charge of negotiations in the 1980s to prevent US banks being dragged under by unpayable debts from Latin American countries. In 1998 it propped up the Long Term Capital Management hedge fund and, most recently, through the Federal Reserve central bank, it has tried to limit the damage caused to the financial system by the subprime mortgage crisis. Indeed, states have intervened more to deal with crises since the 1970s than in the 1960s and 1950s for the simple reason that the crises have been much more severe.
It is true that the inability to stop crises using old “Keynesian” techniques has led to short term attempts to leave things to the market in the belief that “creative destruction” will allow “efficient” capitals to benefit from the weakening or elimination of “inefficient” ones. This is what the Volcker shock – the raising of US interest rates at the end of the 1970s – was supposed to do; it is what the Thatcherites tried to do with high interest rates and restriction of the money supply in 1980–4; it was also, in effect, what the USSR’s ruling nomenklatura embarked on when faced with the great economic, social and political crisis that developed from the mid-1980s onwards. But on each occasion those that survived these attempts turned back to reliance on the state.
The US may be the advanced country where the neoliberal ideology is most entrenched. But it has financed government spending by the “Keynesian” method of borrowing through most of the neoliberal period in a way that it did not do in the Keynesian era. For the US ruling class neoliberalism, in the sense of letting the market rip apart established capitals, is something to be imposed on weaker national capitalisms to the benefit of US capital, not something to be allowed to happen without restriction in the US itself.
The same logic has been followed in Western Europe, Japan, China and, after the wave of not very creative destruction under Yeltsin, Russia. By contrast, the most thorough attempts to implement neoliberal practices have been in the poorer countries of the Global South. Here local ruling classes that entrenched their rule during the “developmentalist” post-war years embrace genuinely neoliberal measures promoted by the International Monetary Fund and World Bank in the hope of becoming junior partners to capitals operating from the industrially advanced countries. [38] But even in these cases tensions can arise, leading to some reassertion of the role of the national state. Certain Latin American countries have taken a “neodevelopmentalist” turn – complete with Keynesian economic advisers – mixing “Keynesian” and “neoliberal” practice in the aftermath of devastating economic, social and political crises. [39]
For these reasons, “neoliberal” is not in reality an accurate description of the operation of capital today. We are not faced with a reversion of the system to the free market capitalism that came to an end more than a century ago. Rather we face a system that attempts to deal with its problems by restructuring on an international scale of the units of the system that emerged in the course of the 20th century – units that Marxists called “monopoly capitalisms”, “state monopoly capitalisms”, or “state capitalisms”. States continue to play a central role in trying to facilitate or regulate this, even if the internationalisation of production makes this much more difficult that in the immediate post-war decades.
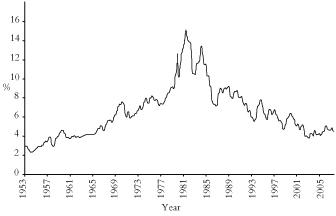
Duménil and Lévy justify their claim that government economic intervention in the past three decades has been in the interests of “finance capital” by referring to the high long term rates of interest that Paul Volcker imposed in 1978, while he was chair of the US Federal Reserve. These high rates were, they argue, “maintained through the 1980s and 1990s”. [40] This ignores the empirical reality. When high interest rates started seriously hurting industry in 1982 Volcker cut them, and the real trend of long term interest rates in the second half of the neoliberal period has been down, not up.
|
Figure 3: Ten-year treasury constant maturity rate |
|
The whole claim that there are two distinct sections of capital – finance capital and industrial capital – is open to challenge. Many important financial institutions not only lend money, but also borrow it, since they are involved in “intermediation” between lenders and borrowers. What matters for them is not the absolute level of interest rates but the gaps that open up between different rates, particularly between long term and short term rates. And industrial concerns lend as well as borrow. Typically they accumulate surpluses between bouts of new investment, which they lend out in return for interest.
One important phenomenon over the past quarter of a century has been a long term decline in the proportion of surplus value going into new productive investment, which is a result of profit rates throughout the system not being fully restored to their early 1970s level. Saving by capital is greater than productive investment [41] – and industrial capitalists have turned to financial ventures in an attempt to use their surpluses profitably. If a greater section of capital is focused on finance than in the past, this is not because something called finance capital has taken control from industrial capital. It is because industrial capital has attempted to restore its profit rates through “financialisation”. At the end of the day this is a blind alley for it, since only productive labour can produce the new value out of which expanded profits can come. It is not that Wall Street has taken over from Main Street, as Harvey asserts. It is that both face problems today that they did not in the immediate post-war decades.
David Harvey’s account of neoliberalism focuses on features that, he claims, lead to a new model of capitalist accumulation – accumulation by “dispossession”, “primitive accumulation”, and the absorption by capital of “non-capitalist” sectors and societies. Accumulation by dispossession is, he argues, “the dominant form of accumulating relative to expanded reproduction” [42] and takes a wide range of forms:
Harvey’s list includes a range of unpleasant features of contemporary capitalism. But merely describing these as “dispossession” does not explain the present stage of the system. “Dispossession” is simply a long word meaning theft. When Pierre-Joseph Proudhon used the phrase “property is theft” in the 19th century, it was an anti-capitalist rallying cry, capable of expressing people’s indignation at the system; so too is Harvey’s phrase “accumulation by dispossession”. But sloganising against theft is not the same as providing a serious analysis, any more than it was when Marx criticised Proudhon in 1847.
The problem with Harvey’s analysis is all the more serious because it includes features that have always accompanied capitalist accumulation, like the “dispossession” of some capitals by others in the course of the recession-boom-recession cycle, as well as attacks on wages and working conditions. It also includes methods that some capitalists use to expand their profits at the expense of other capitalists such as “the dispossession of assets by credit and stock manipulation”. This cannot enable the capitalist class as a whole to accumulate more. As Marx put it:
The class of capitalists taken as a whole cannot enrich itself as a class, it cannot increase its total capital, or produce a surplus value, by one capitalist’s gaining what another loses. The class as a whole cannot defraud itself. [44]
What applies to the dispossession of some capitalists by others even applies to certain forms of dispossession of non-capitalist sectors of the population. For instance, the widespread third world phenomenon of forcibly driving the urban poor from inner cities to make fortunes for property developers involves the further oppression of some of the poorest sections of the population. But it does not, in itself, create new value or surplus value for the capitalist class as a whole. The rents charged on luxury flats or office blocks are paid for out of already existing surplus value in the pockets of rich individuals or capitalist corporations. [45]
Harvey argues that dispossession means that “primitive accumulation”, which Marx saw as important at the time of the rise of capitalism, continues to be a central feature of the world today – indeed, it seems, a more important feature than accumulation through the exploitation of labour power. But for Marx primitive accumulation was not simply the building up of fortunes by early capitalists through robbery. It was, centrally, robbery of land from peasants, which then forced them to seek employment as wage workers. Its specificity did not lie in exploiting classes increasing their wealth by force (something that has happened in all sorts of class societies). Crucially, it permitted the development of a specifically capitalist way of expanding this wealth by creating a class of “free” workers with no choice but to sell their labour power to those now in control of the means of production.
This form of “primitive” accumulation does continue today. Old landowners in Egypt, agrarian capitalists in Brazil, local Communist Party bosses in China and recently established capitalist farmers in India are continually trying to grab the land of local peasants, and where they succeed a new proletariat is created. But Harvey is mistaken in claiming this only characterises recent decades. As Terry Byres has noted, primitive accumulation occurred in the colonial empires that persisted into the post-war decades, although it was “far less successful in its separation of the producers from the means of production than domestic primitive accumulation was in Western Europe ... it had also left a large stratum of poor peasants in possession of land”. [46]
While recent decades have seen the crudest forms of primitive accumulation, “it is not obvious that capitalist transformation is proceeding successfully” except in the case of East Asia. [47] For Byres, the only large country where primitive accumulation has added substantially to capital accumulation as such is China, where “from 1978 onwards, millions were driven off the land, i.e. were effectively dispossessed and proletarianised”. [48]
No account of primitive accumulation should leave out the most important in the 20th century – the seizure of the land from the USSR’s tens of millions of peasant families through Stalin’s “collectivisation” of agriculture from 1929 onwards. Harvey refers to this, but cannot include it in his account of the pre-neoliberal capitalist era, since he sees Stalinist-type regimes as attempts “to implement programmes of modernisation in those countries that have not gone through the initiation into capitalist development”.
For Harvey, Marx’s account of “primitive accumulation” is less important than an idea drawn from Rosa Luxemburg. She argued that a shortage of demand for capitalism’s products meant the system could only continue to expand by cannibalising the pre-capitalist world around it. Harvey writes, “The idea that some sort of ‘outside’ is necessary for the stabilisation of capitalism ... has relevance.” He argues that capitalism’s problem is “over-accumulation” and that this can be solved by eating up “non-capitalist social formations or some sector within capitalism that has not yet been proletarianised”. [49]
But what is there “outside capitalism” to allow “accumulation by dispossession” on the necessary scale? Harvey’s answer is that the state constitutes this “outside” – whether it is the state of the so-called “non-capitalist countries”, the developmental state in much of the Third World, or the state sector in advanced capitalist countries. Since these are all, for him, non-capitalist, a shift of their resources into private hands can provide new resources for capitalist accumulation. In making this argument, Harvey chimes with the “common sense” of a good portion of the left internationally, but it is a mistaken common sense.
Already in the 1870s Engels understood that nationalisation does not in itself produce something outside capitalism:
The modern state, no matter what its form, is essentially a capitalist machine, the state of the capitalists, the ideal personification of the total national capital. The more it proceeds to the taking over of productive forces, the more does it actually become the national capitalist, the more citizens does it exploit. The workers remain wage workers – proletarians. The capitalist relation is not done away with. It is rather brought to a head. [50]
In the period following the Second World War all serious Marxist analyses had to take into account intervention by states, not only to support private capitalists, but also to undertake capital accumulation in their own right. For instance, the German Marxist Joachim Hirsch described how:
As the development of the productive forces progresses, the maintenance of the process of accumulation demands, on the one hand, forms and individual capitals of an order of magnitude which capital, to some extent, is no longer capable of bringing forth itself directly in its reproduction process, and which can only be realised through the intervention of the state apparatus. On the other hand, this very process creates the necessity for counteracting state interventions to guarantee a relative equilibrium in the process of reproduction as a whole. [51]
To read Harvey, you would think that the existence of a substantial state sector slowed down accumulation during the post-war decades. But that was a time with a higher rate of accumulation than today, so much so that is has been baptised “the golden age of capitalism”. As Ben Fine notes, “The boom ... was sustained by the opposite of the factors that Harvey now takes to be instrumental in current accumulation, not least the extension of nationalised industries and the economic role of the state more generally”. [52]
There has been a trend towards privatisation of nationalised industries across much of the capitalist world for the past quarter of a century, just as there was a trend in the opposite direction through much of the 20th century. How are we to explain this? A number of distinct factors are involved.
The first moves to privatise state owned industries in the 1980s were often a pragmatic response to “the fiscal crisis of the state” – the pressure on government finances as recession cut into tax revenues, and unemployment forced up dole and social security payments. Selling off state holdings in profitable companies, and then whole state owned corporations, brought in lots of cash and provided short term relief for governments’ problems. It was this that motivated the 1974-9 Labour government to sell shares in Burma Oil and BP.
Combined with this was a belief that state monopolies, removed from the pressure of competition, were not pushing their workers hard enough. This ties in with a wider notion that is often repeated today, even by some on the left – that the period of state economic interventionism was somehow based on a “Fordist” compromise between employers and workers (a view which should be refuted by the actual behaviour of the Ford Motor Company). [53] The logic of this view was that breaking up state owned monopolies and opening them to the market would force their managers to be much harder on the workers, and would intimidate the workers into accepting worse conditions. Certainly the approach of privatisation often encouraged managers to force through methods to push up productivity. And once privatised, it was easy for companies to “contract out” a range of activities, so breaking the links that tie weak groups of workers to potentially more powerful ones. Ben Fine argues that “privatisation has been an important way in which the relations between capital and labour have been reorganised” and is connected to so-called “labour market flexibility”. [54]
But this motivation for privatisation could clash with its use as a short term solution to the state’s financial problems. For the state to make a lot of money out of privatisation, the privatisers had to have a prospect of monopoly profits. The breaking up of firms to shake up managers and frighten workers would do away with the monopoly. In practice most firms were sold intact, and left in a position of being able to charge monopoly prices to other sections of capital. [55] The state then had to appoint “regulators” to try to do by decree what the market was meant to do.
At the same time, privatisation is not absolutely necessary to create the illusion of the automatism of the market. The breaking up of state run institutions into competing units (NHS trusts, foundation hospitals, city academies, “self-governing” colleges, “agencies”) can try to achieve the same goal; so can “market testing” within particular entities. So too can deregulation aimed to produce competition between different nationally based, and often still state owned, companies. This is what the European Union is trying to do to a whole range of industries such as electricity and postal services. The end result of privatisation in a country like Britain can be that whole sections of “privatised” services such as electricity, water and rail can be run by foreign state owned companies.
These last examples refute Harvey’s portrayal of privatisation somehow crossing a magic line from “non-capitalist” to “capitalist” production. They do fit in with his description of neoliberalism as concerned with “class power”, although describing this as a “restoration”, let alone a creation, of class power is to massively exaggerate the weakness of the capitalist class in the pre-neoliberal period. There is also considerable debate about how effective privatisation has really been. Keynesian pro-capitalist analysts have produced studies suggesting zero or very few gains to “efficiency” from privatisation compared to changes such as new technology that could have been introduced just as effectively, perhaps even more effectively, in a nationalised concern.
Class power is involved in privatisation in another way. A powerful ideological myth sustaining capitalist rule within bourgeois democracies is that the state represents the whole of the population. To sustain this myth the ruling class has to concede a margin of influence to the mass of people over the behaviour of the state through elections. This was not a problem when the general level of profitability allowed it to grant real reforms. Indeed, state possession of industries could help sustain the myth that the state was neutral in relation to class forces, so stabilising capitalism politically as well as economically. But when capitalism entered a long period of crises three decades ago a risk arose that people would expect the state controlled section of industry to protect them against the impact of these crises. Separating industry off from the state and subjecting it to the market can depoliticise the attacks on workers that accompany the crisis, shifting the blame to the seemingly automatic, natural forces of the market.
So Gavriil Popov, the free market economist who was mayor of Moscow during the tumultuous years 1989 to 1992, argued:
If we cannot soon denationalise and privatise property, we will be attacked by waves of workers fighting for their own interests. This will break up the forces of perestroika and put its future in question ... We must seek new mechanisms and institutions of political power that depend less on populism. [56]
This Russian example challenges Harvey’s ideas that “non-capitalist states” were transformed into capitalist ones to the benefit of the world system as a whole between 1989 and 1991. Far from this seeing the “creation” of a new class, many of the same people continued to control industry and the state. Faced with a great social crisis, they sought to find a way out by restructuring the economy under their control, and to protect themselves, through forms of privatisation giving the impression of ownership by the mass of people (for instance, privatisation by distributing vouchers, which favoured industrialists and apparatchiks who could then buy them up on the cheap). Some of the old ruling class gained from this and some lost out. But it can hardly be argued that the result was a great boost to accumulation either in the former USSR or worldwide – accumulation rates worldwide fell in the 1990s to even lower levels than in the 1980s. [57]
The almost “giveaway” privatisations of 1980s Britain, when firms and housing stock were sold below their real value, had the additional ideological advantage of winning support from sections of the middle class and some workers. However, this was not nearly as powerful a force as those who talked in the mid-1980s about “authoritarian populism” used to claim. For instance, one 1980s study found that workers who bought their council houses were no more likely to vote Tory than those who had not. [58] Harvey overstates the case when he writes that under Thatcher “middle class values spread more widely to encompass many of those who had once had a firm working class identity”. [59]
There are two more factors involved in the trend towards privatisation. Many commentators hold that it makes restructuring through mergers and acquisitions across national boundaries easier. As Ben Fine has argued, restructuring internationally “has posed a problem to state owned industries which are confined to domestic ownership alone”. [60] For capitalists involved in such activities, there is always the suspicion that a state owned partner will be getting tax concessions and subsidies from its government which will distort its balance sheets – and that if the merged company faces economic difficulties that government will come under political pressure to try to pass the buck to the foreign partner.
This element in the logic of privatisation is particularly appealing to those best placed to gain from it. Privatisation imposed on Third World countries by the International Monetary Fund and the World Bank as the price of deferring debt repayments can be of considerable benefit to American and European capital. Harvey quite rightly makes this point. He is, however, mistaken when he gives the impression that this form of “accumulation by dispossession” is somehow central to profit making.
An indication of where capital can best gain profits is given by the global flows of foreign direct investment. Two thirds of these are to the advanced countries, and the biggest chunk of the rest is to one destination only – China. The fact that those non-Western countries with financial surpluses (China, the Gulf oil states, etc.) have been using them to finance “private equity” takeovers of Western firms suggests that they know where most of the lucre still lies. [61]
Finally, privatisation is very profitable for some capitalists. It cannot in itself create more surplus value. Only increasing the exploitation of workers or peasants can do that. Otherwise all that is involved is diverting surplus value from one capitalist to another. But it does benefit particular capitalists. Their material interests are very much connected with the propagation of neoliberal ideology, and they set out to woo, bribe and browbeat politicians into pushing privatisation further.
There is always a certain danger in propagandising and agitating against repeated capitalist offensives. In stressing the harm they do it is very easy to overestimate their success and to underestimate the obstacles confronting them. It is also easy to forget that these obstacles come not only from popular resistance, but from contradictions within capitalism itself. A picture is presented of a defeated working class, no longer capable of withstanding the onslaught on its conditions. The typical worker is said to suffer precarious employment, with the threat continually hanging over his or her head of the firm simply shutting down and moving abroad.
So John Holloway asserts, “Capital can move from one side of the world to the other within seconds”. [62] Hardt and Negri’s Empire claims, “Capital can withdraw from negotiation with a given local population by moving its site to another point in the global network ... Entire labouring populations have thus found themselves in increasingly precarious employment situations”. [63] For Harvey, capital relocates production as one of the “spatial temporal fixes” through which it responds to over-accumulation: “The geographical mobility of capital permits it to dominate a global labour force whose own geographical mobility is constrained”. [64] With technological change “offshore produc-tion became possible and the search for profit made it probable. Wave after wave of deindustrialisation hit industry after industry and region after region within the US”. [65] This, he claims, enables capital to impose increasingly precarious forms of work on workers:
In the neoliberal scheme of things short term contracts are preferred in order to maximise flexibility ... Flexible labour markets are established ... The individualised and relatively powerless worker then confronts a labour market in which only short term contracts are offered on a customised basis. Security of tenure becomes a thing of the past. Under neoliberalisation, the figure of “the disposable worker” emerges as prototypical upon the world stage ... Disposable workers – women in particular – survive both socially and affectively in a world of flexible labour markets and short term contracts, chronic job insecurities, lost social protections, and often debilitating labour, amongst the wreckage of collective institutions that once gave them a modicum of dignity and support. [66]
This picture is not unique to left critics of neoliberalism. It is also to be found in the writings of those who have abandoned the left to embrace some version of the “Third Way”. Some of the phrases in Harvey could almost come from the writings of Anthony Giddens or Manuel Castells. [67] Castells, for instance, writes of:
Structural unstability [sic] in the labour markets everywhere, and the requirement for flexibility of employment, mobility of labour, and constant reskilling of the workforce. The notion of the stable, predictable, professional career is eroded, as relationships between capital and labour are individualised and contractual labour conditions escape collective bargaining. [68]
So many different voices tell the story that, it seems, no amount of counter-evidence can stop people believing in it. [69] For instance, Harvey, writing 18 years ago, admitted that such counter-evidence exists, referring to the empirical work of Anna Pollert who “challenges the ideas of flexibility in labour markets and labour organisation and concludes the ‘discovery of the flexible workforces is part of an ideological offensive which celebrates pliability and casualisation and makes them seem inevitable’”. [70] His response was simply to dismiss such evidence out of hand: “I do not accept this position. The evidence for increased flexibility (subcontracting, temporary and self employment, etc) through the capitalist world is simply too overwhelming to make Pollert’s counter-examples credible”. [71] He did not himself provide such evidence, and does not in his later books either.
I have challenged the sorts of claims Harvey takes for granted before and do not intend to lay out the evidence once more here. [72] But certain important points need to be made:
In other words, it is in the interests of employers to overemphasise how precarious jobs are in order to demoralise workers and lower the level of resistance. The task of the left is not to exaggerate insecurity, but to point to the counter-factors that provide workers with continued strength if they have the confidence to deploy it.
There is an assumption in most anti-neoliberal writing that we are living through a period of the “withdrawal of state from social provision”, as Harvey puts it. [81] But once again empirical evidence does not back up such assertions, particularly for the advanced industrial countries. State expenditure on social provision, like state expenditure in general, has, if anything, tended to rise through the decades since the 1970s (see figure 4).
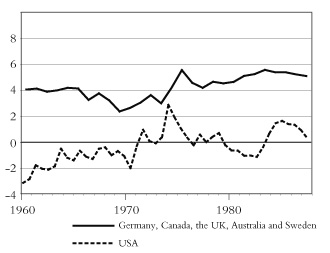
Since 1995 expenditure on “social protection” by the main European countries has been more or less fixed, going up and down slightly with unemployment levels, and was no lower in the most recent US recessions than previous ones, despite “welfare reform” in the Clinton presidency. An analysis by Anwar Shaikh calculated the “net social wage” – the value of social expenditure from which workers benefit minus the taxes which workers pay – in a number of countries. [82] He found that, for Germany, Canada, the United Kingdom, Australia and Sweden combined, this net social wage was generally higher as a proportion of GNP in the 1980s than in the 1960s and 1970s; the trend was similar in the US (figure 5).
|
Figure 4: Welfare expenditure as percent |
||
|
Country |
1979 |
1995 |
|---|---|---|
|
Australia |
13.2 |
16.1 |
|
Canada |
14.5 |
18.0 |
|
France |
22.0 |
29.1 |
|
Germany |
25.4 |
28.7 |
|
Italy |
21.2 |
22.8 |
|
Sweden |
25.1 |
34.0 |
|
United Kingdon |
16.4 |
22.5 |
|
United States |
13.8 |
15.8 |
|
Figure 5: Net social wage as percent of GNP |
|
Shaikh’s analysis also makes a very important point. The bulk of “social wage” expenditure has always been paid for out of taxes on ordinary wages. In effect, it amounts to a redistribution of wage income within the working class – and in the US in the 1950s and 1960s, when the net social wage was negative, it amounted to workers providing a subsidy to the state rather than vice versa. Noting the variation between countries he writes:
Unlike the United States, the other OECD countries had generally positive net social wage ratios. Germany and the United Kingdom had the highest ratios, though even they averaged only about 5 percent of GDP and about 8 percent of total wages. Second, Sweden, the very paradigm of a welfare state, had an average net social wage around zero over the boom period. [84]
There have been repeated attempts by governments to cut back on social expenditures over the past three decades. Indeed in Britain struggles against cutbacks began much earlier than that. [85] Yet the expenditures have gone on rising. How is that to be explained?
Part of the explanation has to do with struggles against the cutbacks. So long as governments depend on elections in bourgeois democracies, they cannot completely ignore the impact of their policies on the lives of the mass of the population. So in Britain the prominence of the NHS in successive general elections led New Labour to increase the proportion of GNP going into it. Harvey is right to highlight “the balance of class forces” in determining the degree of neoliberalisation. [86] But that is not the end of the story. There are features built into capitalism that compel it to pay out a social wage even though it resents doing so.
Capitalist ruling classes can only prosper by exploiting people’s capacity to work (their “labour power”). That capacity is damaged by illness, accidents and malnutrition. So capitalists have to worry about keeping a fit and able body of workers (i.e. “reproducing labour power”). That requires healthcare for workers, and benefits to enable workers to survive through periods of unemployment so that they can be fit for exploitation when the economy revives.
Modern capitalism also has to worry about the upbringing of the next generation of labour power, and ensuring it has the right level of education, training and work discipline to be profitably exploited. Hence the way its apologists worry about the “human capital” of the workforce and the amount of educational “value added” by schools. Finally, it is not just a question of physical wellbeing and aptitude. It is also a question of morale. The capitalist wants contented workers to exploit in the same way that a farmer wants contented cows. Workers cannot be expected to labour with any commitment to their work if they expect to starve to death once they reach retirement age. As Marx put it, there is a historically and socially determined element to the cost of reproducing labour power as well as a physiological one.
A pivotal moment in welfare development in Britain was the panic that developed at the time of the Boer War, when it was discovered that a high proportion of those who tried to enlist in the armed forces were not fit enough to fight. Ann Rogers has summarised the upper and middle class reaction:
The belief that change was necessary if Britain was to compete successfully with Germany and the United States remained central. Whether the argument was formulated by the Fabians or by Liberal imperialists the concentration was on the damage that poverty was doing to society rather than the misery it caused individual workers ... the underlying reason for the desire to improve the health of the working class was the need for a healthier labour force in the factories and the army. [87]
This was the background to the granting of old age pensions and the provision of school meals by the Liberal government of 1906.
But labour power is not an object like other commodities, which are passive as they are bought and sold. It is the living expression of human beings. What from a capitalist point of view is “recuperation of labour power” is for the worker the chance for relaxation, enjoyment and creativity. There is a struggle over the social wage just as over the normal wage, even if both are, up to a certain degree, necessary for capital.
This makes it very difficult for capital to redesign the welfare state in a way which would really fit with its narrow economic requirements. That would involve maintaining and even expanding those of its elements that are essential to the maintenance and reproduction of a productive labour force, while curtailing or abandoning “non-productive” expenditure on things like the care of the chronic sick, of the seriously disabled and of retired workers. The competitive extraction of surplus value demands the continuation of part of the welfare state. The political realities of maintaining power through bourgeois democracy rule out dismantling the rest of it.
This is where internal markets, market testing, contracting out, privatisation, encouraging private pensions and all the rest come in. They are mechanisms that are meant to depoliticise the process of social provision, so making it easier to refuse it to those deemed not to deserve it on the one hand, and to clamp down on the workers in the welfare sector on the other.
Why do these arguments matter if we are all agreed that marketisation, privatisation and precariousness are bad things? They matter because mis-analysis leads to serious mistakes when it comes to fighting back. If the centre of accumulation has moved from day to day exploitation to “dispossession”, then the focus of the fight shifts from the working class to struggles of those who are marginal to the productive process. The shift in focus is further reinforced if almost all jobs are seen as precarious, with employers being able to dismiss any workers who rebel. This is what Harvey seems to be arguing when he writes that in the post-1973 world “accumulation by dispossession moved to the fore as the primary contradiction within the imperialist organisation of capital accumulation”. [88]
Such an analysis puts a stress on “social movements” as opposed to class movements. [89] The writers who have gone furthest in drawing such a conclusion are Laclau and Mouffe who write that the “overdetermination assumed by social struggles in the third world” involves “the construction of political identities having little to do with strict class boundaries”. [90] Harvey resists this conclusion, at points insisting that class is central to resistance, but his theoretical framework leaves it open to an interpretation little different from that of Laclau and Mouffe. This has important practical implications. Struggles of social movements tend to rise rapidly and then fall back just as rapidly precisely because they are not based on those whose position within the structures of capitalist production binds them together organically and provides them with the power to confront the system. As the saying goes, social movements “rise like a rocket and fall like a stick”. What are left behind are skeleton organisations that are too weak to achieve their goals. Those involved are then all too easily tempted to conclude that a struggle cannot lead to victory, and to put their faith in reforms within the existing society, whether through old style reformist and populist parties or through NGOs.
Instructive in this regard are the arguments used by Fausto Bertinotti of Rifondazione Comunista in Italy to justify his turn to a government coalition with the pro-capitalist “centre-left” led by Romano Prodi. His turn came as the wave of demonstrations that occurred between the Genoa G8 protest (July 2001) and the start of the Iraq war (March 2003) began to decline, and in the wake of the failure to gain enough votes in a referendum on workers’ rights for it to pass into law. He painted a picture of the popular movements in Italy risking devastating defeats because precariousness had sapped people’s capacity to fight back:
The basic thing that characterises neoliberal globalisation is precariousness. It conditions the time devoted to labour and life, the relations of production and social relations, and which even penetrates into attempts to modify the people’s lives. [91]
What was involved in Rifondazione’s shift was not just the capitulation – or betrayal – of one individual. Crucial was his capacity to convince many thousands of activists to accept his arguments. This was possible because Rifondazione’s activists had long been influenced by certain autonomist and Eurocommunist ideas that held that the working class’s strength had been damaged permanently by the mobility of capitalism and the “deindustrialisation” and “precarity” it produced. Social movements were seen as the only way forward, and when they went into decline the only hope seemed to be entering a government which might make at least a little turn away from “neoliberalism”. Much the same happened to some of the semi-autonomist left in Argentina after the great revolt of December 2001 to January 2002. Once the great upsurge of the social movements of piqueteros and the popular assemblies died down, the easy option seemed to be to work with the Kirchner government as it made its turn away from the radical version of neoliberalism of the previous decade.
Such shifts, from radical opposition to working through parties and governments that try to manage the system for capitalism, are encouraged by the notions of a “good” “Keynesian” version of capitalism and a “bad” “neoliberal” one – or the parallel contrast between “finance capital” that does not care for workers and “productive capital” that supposedly does. The reality is that capital uses the state as much today as it did in the heyday of “Keynesianism” – indeed, even more so, insofar as it is faced with more crises needing intervention. Neoliberalism as an ideology does not guide practice when it comes to this matter. The difference with the post-war decades is that capital is anxious to cut back on many of the positive reforms it granted in a more profitable era, and states respond accordingly.
It is this which leads to the ambiguities in the use of the term “neoliberalism” by the left. The term can be used simply to designate the negative features of many governmental measures in the present phase of the system – the anti-reforms that have replaced the positive reforms it was possible to extract from capital without a great deal of struggle from the late 1940s to the mid-1970s. But the term can also be used to reinforce the illusion that minor changes in the running of parts of the system are all that is necessary to improve the situation of the mass of people. By the same token, those who see their fight as an “anti-neoliberal” one can move on to see it as “anti-capitalist”, but they can also slip back into conciliation with the system. Rhetoric and slogans have a role in politics, but they are not a substitute for clarity about the enemy and how to fight it. And we will all need more clarity as the competitive pressures on national states and capitalist firms in a period of recurrent crises leads to more attacks on the wage, the social wage, working conditions and jobs.
1. This article is based on research for a forthcoming book. I would appreciate suggestions and constructive criticism. Please email chrisharman@swp.org.uk
2. It is not to be found in earlier works dealing with the same phenomenon, such as Harvey, 1989, or Harman, 1995.
3. Pierre Tartakowsky, speaking at a fringe meeting at the National Union of Students conference in Blackpool, April 2000.
4. Interview in Socialist Review 242 (June, 2000).
5. Bourdieu, 1998, pp. 6–7.
6. George, 1999, p. 184.
7. Harman, 2000, p. 55.
8. Harman, 2000, p. 55.
9. Callinicos and Nineham, 2007.
10. Bensaïd and Rousset, 2007, p. 25 (my translation).
11. I did so at some length seven years ago, see Harman, 2000.
12. Their explanation is different to Marx’s. See my comment in Harman, 2007a.
13. Duménil and Lévy, 2004a, p. 86.
14. Duménil and Lévy, 2004a, p. 186.
15. Chesnais, 1997, p. 74. The passages from Chesnais are my translations.
16. Chesnais, 1997, p. 304.
17. Harvey, 2005, p. 10.
18. Harvey, 2005, p. 11.
19. Harvey’s account is based on a passage in the third volume of Marx’s Capital. But, for Marx, over-accumulation occurs at one phase of the slump-boom cycle. When the boom reaches its height, capital accumulation exceeds the resources of labour power needed to sustain it by providing surplus value to maintain the rate of profit. This leads to the production of more commodities than the system can absorb. In Marx’s account the resulting crisis removes over-accumulation. For Harvey overproduction seems to be a permanent condition, but he does not explain how this is possible. To do so he would have to examine the nature of the capitalist cycle today and its impact on the rate of profit.
20. Harvey, 2005, p. 16,
21. Harvey, 2005, p. 72. See also p. 36 and p. 76.
22. Harvey, 2005, p. 33. In making this argument, Harvey goes in the opposite direction to most of those who emphasise finance capital. They focus instead on a shift towards “shareholder power”.
23. Harvey, 2005, pp. 152–153.
24. Harvey, 2003, pp. 75–76.
25. Duménil and Lévy, 2004a, p. 201.
26. Some neoliberals reject the part of neoclassical theory that rules out crisis, basing themselves on the so-called “Austrian school” that sees crises as an indispensable part of the “creative destruction” of the system. See Harman, 1996a, and Chang, 2002.
27. For the shift to various versions of Keynesianism, see Harman, 1996a.
28. Campbell, 2005, p. 189.
29. Campbell, 2005, p. 188.
30. Matthews, 1968, p. 556. See also Tomlinson, 1981.
31. The Guardian, 26 September 1983.
32. Campbell, 2005, p. 189.
33. Friedman’s contention that the state had an important role to play in managing the money supply was seen as almost tantamount to Keynesianism by some of the “new classical economists”. See Garrison, 1992.
34. Bukharin, 1927.
35. The Czechoslovakian recession of the 1960s, followed by the Polish crisis of the mid-1970s showed that even the most extreme forms of state intervention could not sustain accumulation indefinitely. See Harman, 1977.
36. United Nations Economic and Social Council, basic data on government expenditure and taxation, February 2004.
37. Harman, 2007b.
38. For more on this, see Harman, 2003.
39. Katz, 2007.
40. Duménil and Lévy, 2005, p. 13.
41. There is a detailed examination of these trends in Terrones and Cardarelli, 2005.
42. Harvey, 2003, p. 153.
43. These methods are referred to in Harvey, 2003, pp. 145–147.
44. Marx, 1987.
45. This point is made in Fine, 2006.
46. Byres, 2005, p. 84.
47. Byres, 2005, p. 87.
48. Byres, 2005, p. 88.
49. Harvey, 2003, p. 141. Another of his “fixes” is investment in long term infrastructure projects within capitalism. It is these that he sees as absorbing “excess” capital and labour during the early post-war decades, although without explaining how they maintained the profitability of capital. His argument in some ways resembles that of Baran and Sweezy in Monopoly Capital – but unlike them Harvey hardly mentions the huge sums spent on arms in A Short History of Neoliberalism, The New Imperialism or his earlier The Condition of Postmodernity. It is this omission that allows him to conceive of a peaceful “spatial fix” for capitalism today. For an acute criticism of his argument, see Fine, 2006, pp. 143–144.
50. Engels, 1897, pp. 71–72.
51. Hirsch, 1987, pp. 81–82.
52. Fine, 2006, p. 145.
53. See for instance, Dunn, 2004, pp. 63–64 and 66–67.
54. Fine, 1999, p. 42.
55. Witness the bitter complaints of Ryanair’s ultra-Thatcherite boss Michael O’Leary against BAA’s monopoly charges for using London’s main airports.
56. Quoted in Socialist Review, December 1990.
57. See the figures in Terrones and Cardarelli, 2005.
58. Heath, Jowell and Curtice, 1985.
59. Harvey, 2005, pp. 61–62.
60. Fine, 1999, p. 42.
61. Duménil and Lévy have completely distorted the picture in one of their widely read articles. They assert that “in 2000, US financial investments (treasury bills, bonds, commercial paper, stock shares, direct investment, etc.) in the rest of the world amounted to 3,488 billion dollars. The corresponding income was 381 billion dollars, that is, a return of nearly 11 percent. It is interesting to note that this income was approximately equal to the total after-tax profits of all corporations in the United States, excluding such flows from abroad – that is a ratio of 100 percent” (Duménil and Lévy, 2004b). This is a complete misuse of figures, since it ignores foreign investments in the US and the counterflow of income from the US to capitalists and states abroad. Inward investment into the US has for some years been considerably greater than outward investment from it – even if the outward investment is on average more profitable. Duménil and Lévy recognise this elsewhere, giving figures showing income flows into and out of the US balancing each other. See the graph reproduced in Harvey, 2005, p. 191.
62. Holloway, 1995, p. 125. Holloway does at one point recognise that productive capital is loss mobile than money capital, but then goes on to ignore the effect of this distinction on the relations between capitals and states.
63. Hardt and Negri, 2001, pp. 296–297.
64. Harvey, 2005, pp. 168–169.
65. Harvey, 2003, p. 64.
66. Harvey, 2005, pp. 169-170.
67. See Giddens, 1998; Giddens, 2002; Castells, 2006.
68. Castells, 2006, p. 9.
69. See for instance, the article by the journalist John Harris, The Slow Death of the Real Job is Pulling Society Apart, the Guardian, 19 October 2007.
70. Harvey, 1989, p. 190.
71. Harvey, 1989, p. 191.
72. See Harman, 1996b; Harman, 2002. See also Dunn, 2004, and Bellofiore, 1999.
73. Harvey, 2003, p. 100.
74. Koechlin, 2006.
75. Baily and Lawrence, 2004.
76. See, for example, Selwyn, 2007, on Brazilian agricultural workers.
77. Bodin, 2001.
78. Taylor, 2002.
79. These figures are from the Office for National Statistics, Social Trends 2001, p. 88. An excellent, but as yet unpublished, study of the transformation of work by Kevin Doogan provides a similar picture to these figures.
80. Bronfenbrenner, 2000.
81. Harvey, 2005, p. 161.
82. Shaikh, 2003.
83. Drawn from Swank and Martin, 2001, pp. 917–918.
84. Shaikh, 2003.
85. I remember reading about the first cuts in old copies of left wing publications from the early 1950s.
86. Harvey, 2005, p. 50.
87. Rogers, 1993. This article provides an excellent account of the different forces involved in the rise of the welfare state and the current pressures on it.
88. Harvey, 2003, p. 172.
89. There is a confusion in the use of the term “social movements” in some European countries because it lumps together struggles waged along class lines against exploitation with those against oppression and war that appeal, to some extent, across class lines.
90. Laclau and Mouffe, 1985, p. 13.
91. Fausto Bertinotti, 15 Tesi per il Congresso di Rifondazione Comunista, Liberazione, 12 September 2004 (my translation).
Baily, Martin Neil, and Robert Z. Lawrence, 2004, What Happened to the Great US Job Machine? The Role of Trade and Offshoring, paper prepared for the Brookings Panel on Economic Activity, 9–10 September 2004, http://ksghome.harvard.edu/~RLawrence/BPEA%20Baily-Lawr%20Oct%208%20clean.pdf.
Bellofiore, Riccardo, 1999, After Fordism, What? Capitalism at the End of the Century: Beyond the Myths, in Riccardo Bellofiore (ed.), Global Money, Capital Restructuring, and the Changing Patterns of Labour (Edward Elgar).
Bensaïd, Daniel, and Pierre Rousset, 2007, Un Etrange Bilan, Que Faire 6 (September/November 2007).
Bodin, Raymond-Pierre, 2001, Wide-ranging Forms of Work and Employment in Europe, ILO report, www.ilo.org/public/english/bureau/inst/download/bodin.pdf.
Bourdieu, Pierre, 1998, Acts of Resistance: Against the New Myths of our Time (Polity).
Bronfenbrenner, Kate, 2000, Uneasy Terrain: The Impact of Capital Mobility on Workers, Wages, and Union Organising, The ILR Collection, http://digitalcommons.ilr.cornell.edu/cgi/viewcontent.cgi?article=1001&context=reports.
Bukharin, Nikolai, 1927, Economic Theory of the Leisure Class, www.marxists.org/archive/bukharin/works/1927/leisure-economics/.
Byres, Terry, 2005, Neoliberalism and Primitive Accumulation in less Developed Countries, in Alfredo Saad Filho and Deborah Johnston, Neoliberalism, A Critical Reader (Pluto).
Callinicos, Alex, and Chris Nineham, 2007, At an Impasse: Anti-capitalism and the Social Forums Today, International Socialism 115 (Summer 2007), www.isj.org.uk/index.php.4?id=337.
Campbell, Al, 2005, The Birth of Neoliberalism in the United States, in Alfredo Saad Filho and Deborah Johnston (eds), Neoliberalism, A Critical Reader (Pluto).
Castells, Manuel, 2006, The Network Society: From Knowledge to Policy, in Manuel Castells and Gustavo Cardoso (eds.), The Network Society (Center for Transatlantic Relations).
Chang, Ha-Joon, Breaking the Mould: An Institutionalist Political Economy Alternative to the Neoliberal Theory of the Market and the State, Cambridge Journal of Economics 26 (2002), also available online from www.unrisd.org.
Chesnais, François, 1997, La Mondialisation du Capital (Syros).
Duménil, Gerard and Dominique Lévy, 2004a, Capital Resurgent: Roots of the Neoliberal Revolution (Harvard University).
Duménil, Gerard and Dominique Lévy, 2004b, The Economics of US Imperialism at the turn of the 21st Century, Review of International Political Economy, volume 11, number 4.
Duménil, Gerard, and Dominique Lévy, 2005, The Neoliberal Counterrevolution, in Alfredo Saad Filho and Deborah Johnston (eds), Neoliberalism, A Critical Reader (Pluto).
Dunn, Bill, 2004, Global Restructuring and the Power of Labour (Palgrave).
Engels, Frederick, 1897, Socialism: Scientific and Utopian (Allen and Unwin), www.marxists.org/archive/marx/works/1880/soc-utop/.
Fine, Ben, 1999, Privatisation: Theory and Lessons for the United Kingdom and South Africa, in Andriana Vlachou (ed), Contemporary Economic Theory: Radical Critiques of Neoliberalism (Macmillan).
Fine, Ben, 2006, Debating the ‘New’ Imperialism, Historical Materialism, volume 14, number 4.
Garrison, Roger, 1992, Is Milton Friedman a Keynesian?, in Mark Skousen (ed.), Dissent on Keynes (Praeger), available online: www.auburn.edu/~garriro/fm2friedman.htm.
George, Susan, 1999, The Lugano Report: On Preserving Capitalism in the Twenty-first Century (Pluto).
Giddens, Anthony, 1998, The Third Way: Renewal of Social Democracy (Polity).
Giddens, Anthony, 2002, Runaway World (Profile).
Hardt, Michael, and Antonio Negri, 2001, Empire (Harvard), www.angelfire.com/cantina/negri/HAREMI_unprintable.pdf.
Harman, Chris, 1977, Poland and the Crisis of State Capitalism, International Socialism 94 and 95 (old series).
Harman, Chris, 1995, Economics of the Madhouse: Capitalism and the Market Today (Bookmarks).
Harman, Chris, 1996a, The Crisis of Bourgeois Economics, International Socialism 71 (Summer 1996), http://pubs.socialistreviewindex.org.uk/isj71/harman.htm.
Harman, Chris, 1996b, Globalisation: A Critique of a New Orthadoxy, International Socialism 73 (Winter 1996), http://pubs.socialistreviewindex.org.uk/isj73/harman.htm.
Harman, Chris, 2000, Anti-capitalism: Theory and Practice, International Socialism 88 (Autumn 2000), http://pubs.socialistreviewindex.org.uk/isj88/harman.htm.
Harman, Chris, 2002, The Workers of the World, International Socialism 96 (Autumn 2002), http://pubs.socialistreviewindex.org.uk/isj96/harman.htm.
Harman, Chris, 2003, Analysing Imperialism, International Socialism 99 (Summer 2003), http://pubs.socialistreviewindex.org.uk/isj99/harman.htm.
Harman, Chris, 2007a, The Rate of Profit and the World Today, International Socialism 115 (Summer 2007), www.isj.org.uk/index.php.4?id=340.
Harman, Chris, 2007b, Snapshots of Capitalism Today and Tomorrow, International Socialism 113 (Winter 2007), www.isj.org.uk/index.php.4?id=292.
Harvey, David, 1989, The Condition of Postmodernity: An Enquiry into the Origins of Cultural Change (Blackwell).
Harvey, David, 2003, The New Imperialism (Oxford University).
Harvey, David, 2005, A Brief History of Neoliberalism (Oxford University).
Heath, Anthony, Roger Jowell and John Curtice, 1985, How Britain Votes (Pergamon Press).
Hirsch, Joachim, 1987, The State Apparatus and Social Reproduction, in John Holloway and Sol Piccioto, State and Capital: A Marxist Debate (Edward Arnold).
Holloway, John, 1995, Global Capital and the National State, in Werner Bonefeld and John Holloway (eds.), Global Capital, National State and the Politics of Money (St Martin’s).
Katz, Claudio, 2007, El Giro de la Economía Argentina (Parte I), www.aporrea.org/internacionales/a30832.html.
Koechlin, Tim, 2006, US Multinational Corporations and the Mobility of Productive Capital: A Skeptical View, Review of Radical Political Economics, volume 38, number 3.
Laclau, Ernesto, and Chantal Mouffe, 1985, Hegemony and Socialist Strategy: Towards a Radical Democratic Politics (Verso).
Marx, Karl, 1987, The 1861-63 notebooks, in Karl Marx and Frederick Engels Collected Works, volumes 28-30 (Lawrence and Wishart), www.marxists.org/archive/marx/works/1861/economic/.
Matthews, Robin, 1968, Why has Britain had Full Employment since the War?, The Economic Journal, volume 78, number 311 (September 1968).
Rogers, Ann, 1993, Back to the Workhouse, International Socialism 59 (summer 1993).
Selwyn, Ben, 2007, Labour Process and Workers’ Bargaining Power in Export Grape Production, North East Brazil, Journal of Agrarian Change, volume 7, number 4 (October 2007).
Shaikh, Anwar, 2003, Who Pays for the ‘Welfare’ in the Welfare State?, Social Research, volume 70, number 2, http://homepage.newschool.edu/~AShaikh/welfare_state.pdf.
Swank, Duane, and Cathie Jo Martin, 2001, Employers and the Welfare State, Comparative Political Studies, volume 34, number 8.
Taylor, Robert, 2002, Britain’s World of Work: Myths and Realities, ESRC Future of Work Programme Seminar Series, www.esrc.ac.uk/ESRCInfoCentre/Images/fow_publication_3_tcm6-6057.pdf.
Terrones, Marco, and Roberto Cardarelli, 2005, Global Imbalances: A Saving and Investment Perspective, in World Economic Outlook 2005, International Monetary Fund, www.imf.org/external/pubs/ft/weo/2005/02/pdf/chapter2.pdf.
Tomlinson, Jim, 1981, The ‘Economics of Politics’ and Public Expenditure: a Critique, Economy and Society, volume 10, number 4 (November 1981).
Last updated on 7 May 2021