
Leest u dit met een smartphone?
Met (enkele) smartphones moet u zelf uitmaken welke modus voor u geschikt is

Leest u dit met een smartphone?
Met (enkele) smartphones moet u zelf uitmaken welke modus voor u geschikt is
Thomson en Tait, Nat. Philos. I, p. 191 (§ 276):
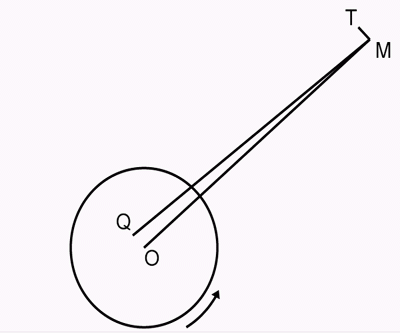
“Alle lichamen waar de vrije oppervlakken deels uit een vloeistof bestaan, zoals de aarde, hebben indirecte weerstanden als gevolg van wrijving, waardoor de bewegingen van eb en vloed worden gehinderd. Zolang zulke lichamen zich ten opzichte van naburige lichamen bewegen, onttrekken deze weerstanden voortdurend energie aan hun relatieve bewegingen. Kijken we eerst naar het effect van de maan op de aarde, met haar zeeën, meren en rivieren, dan zien we dat dit effect de neiging heeft de periodes van de aardrotatie om zijn as en de rotatie van de beide lichamen samen om hun inertiecentrum [Trägheitsmittelpunkt] te egaliseren, want zolang deze periodes verschillen, hebben eb en vloed een effect op het aardoppervlak door het voortdurend onttrekken van energie uit de bewegingen van beiden. Om het onderwerp in detail te bekijken en tegelijk onnodige complicaties te vermijden, veronderstellen we dat de maan een uniform bolvormig lichaam is. De wederzijdse actie en reactie tussen zijn massa en die van de aarde zal equivalent zijn aan één enkele kracht die in om het even welke lijn door het middelpunt beweegt en zo teweegbrengt dat de rotatie van de aarde wordt belemmerd, zolang dit gebeurt in een kortere periode dan de beweging van de maan rond de aarde. [cursief van Engels] Zij moet dus een richting hebben die vergelijkbaar is met die van de MQ-lijn in het diagram dat, met een noodzakelijke aanzienlijke overdrijving, zijn OQ-afwijking van het middelpunt van de aarde weergeeft. De kracht die werkelijk op de maan in de richting van MQ werkt kan nu worden voorgesteld als bestaande uit twee delen; de grootte van het eerste deel, dat werkt in de lijn MO die naar het middelpunt van de aarde gaat, wijkt niet merkbaar af van de grootte van de gehele kracht; de richting MT van de naar verhouding zeer kleine tweede component staat loodrecht op MO. Deze laatste kracht is bijna tangentieel aan de baan van de maan, en werkt in de zin van de beweging van de maan. Als zo’n kracht plotseling zou werken, dan zou het eerst de snelheid van de maan verhogen; maar na een bepaalde tijd, als gevolg van deze versnelling, zou de maan zich verder van de aarde hebben verwijderd met zo’n afstand dat, omdat zijn beweging ingaat tegen de aantrekkingskracht van de aarde, hij evenveel snelheid zou hebben verloren als er door de tangentiële versnelling was bereikt.
Het effect van een voortdurende tangentiële kracht, in de zin van de beweging, maar van zo’n kleine omvang, dat het op elk moment slechts een kleine afwijking geeft van de cirkelvormige baan, bestaat uit het geleidelijk vergroten van de afstand tot het centrale lichaam, en het verlies van evenveel kinetische energie van de beweging, als de eigen arbeid tegen de aantrekkingskracht van het centrale lichaam. Het is gemakkelijk om de omstandigheden te begrijpen als je kijkt naar deze beweging rond het centrale lichaam als een zeer langzaam uitdijende spiraalvormige baan. Op voorwaarde dat de kracht omgekeerd evenredig is met het kwadraat van de afstand, zal de tangentiële component van de zwaartekracht tegen de beweging twee keer zo groot zijn als de storende tangentiële kracht die met de beweging meewerkt, en daarom zal de helft van de arbeid tegenin de eerste, gedaan worden door de laatste, en de andere helft door de kinetische energie die uit de beweging wordt gehaald. Het totale effect op de beweging van de maan, van de nu onderzochte speciale storende oorzaak, wordt gemakkelijk gevonden door gebruik te maken van het principe van het impulsmoment [Momente der Bewegungsgrößen]. Zo zien we dat op elk moment van beweging van het inertiecentrum, van de maan en de aarde t.o.v. hun gemeenschappelijk inertiecentruum, op elk moment evenveel impulsmomenten winnen als dat er verloren gaan door de aardrotatie om haar as. De som van de impulsmomenten van de inertiecentrums van de maan en de aarde, zoals zij nu bewegen, is ongeveer 4,45 maal het huidige impulsmoment van de aardrotatie. Het gemiddelde vlak van de eerste is de ecliptica, en daarom is de gemiddelde inclinatie van de assen van de twee momenten ten opzichte van elkaar gelijk aan 23° 27,5’, welke hoek – aangezien we de invloed van de zon op het vlak van de beweging van de maan hier verwaarlozen - aan te nemen is als de werkelijke huidige inclinatie van de twee assen. Het resulterende, of het gehele impulsmoment, is dus 5,38 keer zo groot als die van de huidige aardrotatie, en zijn as heeft een hellingshoek van 19° 13’ ten opzichte van de aardas. Het uiteindelijke resultaat van eb en vloed is dus aarde en maan uniform te laten draaien met de resulterende impulsmomenten rond de resulterende as, alsof ze twee delen van een onbuigzaam lichaam zijn: in deze staat zou de afstand van de maan tot de aarde (ongeveer) toenemen in de verhouding 1:1,46, dus in de verhouding van het kwadraat van het huidige impulsmoment van de inertiecentrums tot het kwadraat van het gehele impulsmoment; de periode van de rotatie zou worden verhoogd in de verhouding van de kubussen van dezelfde grootte, d.w.z. in de verhouding 1:1,77. De afstand zou dus zijn toegenomen tot 347.100 Engelse mijl en de periode tot 48,36 dagen. Waren er geen andere lichamen in het universum waren dan de aarde en de maan, dan konden deze twee lichamen voor altijd in cirkelvormige banen rond hun gemeenschappelijke inertiecentrum bewegen, en tijdens één omwenteling zou de aarde een omwenteling rond haar as voltooien zodat ze altijd met dezelfde kant naar de maan draaide, zodat alle vloeibare delen van haar oppervlak in rust zouden blijven ten opzichte van de vaste delen. Maar het bestaan van de zon zou voorkomen dat een dergelijke toestand permanent is. Want er zou sprake zijn van een zonnevloed [Sonnenfluten], twee keer zo hoog en twee keer zo laag in de periode van de rotatie van de aarde ten opzichte van de zon (d.w.z. twee keer in de zonnedag of, wat hetzelfde zou zijn, in de maand). Maar dit kan niet gebeuren zonder verlies van energie door de wrijving van het vloeibare [cursief van Engels]. Het is niet eenvoudig om het hele verloop van de verstoring in de bewegingen van aarde en maan te schetsen die dit veroorzaken; maar uiteindelijk moet het ertoe leiden dat de aarde, de maan en de zon om hun gemeenschappelijk inertiecentrum draaien als delen van een onbuigzaam lichaam.”
In 1754 gaf Kant voor het eerst aan dat de rotatie van de aarde werd vertraagd door de getijdenwrijving en dat dit pas voltooid zou zijn,
“wanneer haar” (de aarde) “oppervlak in rust zal zijn ten opzichte van de maan, d.w.z. wanneer het rond haar as zal draaien op hetzelfde moment als de maan er omheen draait, dus altijd met dezelfde kant naar haar toe.”
Hij was daarom van mening dat deze vertraging te wijten was aan de getijdenwrijving, dus de aanwezigheid van vloeibare massa’s op de aarde.
“Als de aarde een vrij stevige massa was, zonder enige vloeistof, zou noch de aantrekkingskracht van de zon, noch van de maan de vrije axiale rotatie kunnen veranderen; want het trekt met gelijke kracht zowel aan de oostelijke als westelijke delen van de aarde en veroorzaakt zo geen neiging naar de ene of naar de andere kant; bijgevolg laat het de aarde volledig vrij om haar rotatie ongehinderd voort te zetten alsof er geen externe invloed is.”
Kant kon tevreden zijn met dit resultaat. Alle wetenschappelijke voorwaarden ontbraken toen om dieper in te gaan op het effect van de maan op de aardrotatie. Het duurde bijna honderd jaar voordat de theorie van Kant algemeen geaccepteerd werd, en nog langer voordat werd ontdekt dat eb en vloed slechts het zichtbare effect is van de aantrekkingskracht van de zon en de maan, die de aardrotatie beïnvloedt.
Deze meer algemene visie op de zaak is ontwikkeld door Thomson en Tait. De aantrekkingskracht van de maan en de zon heeft niet alleen invloed op de vloeistoffen van het aardse lichaam of het aardoppervlak, maar op de hele massa van de aarde in het algemeen op een manier die de draaiing van de aarde remt. Zolang de rotatieperiode van de aarde niet samenvalt met de periode van de baan van de maan rond de aarde, heeft de aantrekkingskracht van de maan – om dit eerst te bekijken – tot gevolg dat de twee periodes steeds dichter bij elkaar komen. Als de rotatieperiode van het (relatieve) centrale lichaam langer zou zijn dan de omlooptijd van de satelliet, dan zou de eerstgenoemde geleidelijk aan verkort worden; en als het korter is, zoals het geval is met de aarde, dan wordt het vertraagd. Maar in het ene geval wordt de kinetische energie niet uit het niets gecreëerd, in het andere geval wordt ze ook niet vernietigd. In het eerste geval zou de satelliet dichter bij het centrale lichaam komen en zijn omlooptijd verkorten, in het tweede geval zou hij verder weg bewegen en een langere omlooptijd krijgen. In het eerste geval verliest de satelliet net zoveel potentiële energie door het naderen van het centrale lichaam als het centrale lichaam kinetische energie krijgt tijdens de versnelde rotatie, in het tweede geval krijgt de satelliet precies dezelfde potentiële energie door het vergroten van de afstand als het centrale lichaam kinetische energie verliest tijdens de rotatie. De totale som van dynamische energie, potentieel en kinetisch, in het aarde-maan-systeem blijft hetzelfde; het systeem is vrij conservatief.
Men kan zien dat deze theorie volledig onafhankelijk is van de fysisch-chemische aard van de betreffende lichamen. Het is afgeleid van de algemene bewegingswetten van vrije hemellichamen, waarvan de verbinding tot stand komt door aantrekking in verhouding tot de massa’s en in de omgekeerde verhouding tot het kwadraat van de afstanden. De theorie is blijkbaar ontstaan als een veralgemening van Kants theorie van de getijdenwrijving, en wordt hier door Thomson en Tait voorgesteld als de wiskundige basis ervan. Maar in werkelijkheid – en vreemd genoeg hebben de auteurs daar geen idee van – sluit ze het bijzondere geval van getijdenwrijving uit.
Wrijving is een belemmering voor de beweging van de massa en werd eeuwenlang beschouwd als de vernietiging van een dergelijke beweging, en dus van de kinetische energie. We weten nu dat wrijving en botsing de twee vormen zijn waarin kinetische energie wordt omgezet in moleculaire energie, in warmte. In alle wrijving gaat dus kinetische energie als zodanig verloren om weer op te duiken, niet als potentiële energie in de zin van dynamiek, maar als moleculaire beweging in de vorm van warmte. De kinetische energie die door wrijving verloren gaat, gaat dus in de eerste plaats echt verloren voor de dynamische aspecten van het betreffende systeem. Ze kan pas weer dynamisch effectief worden als ze vanuit de vorm van warmte weer wordt omgezet in kinetische energie.
Hoe staat het dan met de getijdenwrijving? Het is duidelijk dat ook hier het geheel van de kinetische energie van de watermassa’s op het aardoppervlak dankzij de aantrekkingskracht van de maan wordt omgezet in warmte, hetzij door de wrijving van de waterdeeltjes onderling op grond van de viscositeit van het water, hetzij door de wrijving tegen het vaste aardoppervlak en de erosie van de rotsen, weerbastig aan de getijdenbeweging. Van deze warmte wordt alleen het oneindig kleine deel dat bijdraagt aan de verdamping van het wateroppervlak weer omgezet in kinetische energie. Maar ook deze oneindig kleine hoeveelheid kinetische energie, die wordt overgedragen van het totale aarde-maan-systeem naar een deel van het aardoppervlak, blijft in eerste instantie aan het aardoppervlak, onder de daar geldende voorwaarden, en deze omstandigheden leiden ertoe dat alle daar actieve energie één en dezelfde uiteindelijke bestemming bereikt: de uiteindelijke omzetting in warmte en straling in de ruimte.
Voor zover de getijdenwrijving een onmiskenbaar remmend effect heeft op de aardrotatie, gaat de daarvoor gebruikte kinetische energie absoluut verloren aan het dynamische systeem aarde-maan. Het kan dus niet opnieuw verschijnen binnen dit systeem als dynamische potentiële energie. Met andere woorden: van de kinetische energie die wordt gebruikt om de rotatie van de aarde te belemmeren door middel van de aantrekkingskracht van de maan, kan alleen dat deel dat werkt op de vaste massa van het aardse lichaam volledig opnieuw verschijnen als dynamische potentiële energie, en dus worden gecompenseerd door een overeenkomstige toename van de afstand van de maan. Aan de andere kant kan het deel dat op de vloeibare massa’s van de aarde werkt, dat alleen doen voor zover het deze massa’s niet zelf in een beweging brengt die tegengesteld is aan de rotatie van de aarde, want zo’n beweging wordt volledig omgezet in warmte en gaat uiteindelijk verloren aan het systeem door de straling.
Wat geldt voor de getijdenwrijving aan het aardoppervlak, geldt ook voor de soms hypothetisch veronderstelde getijdenwrijving van een veronderstelde vloeibare kern van de aarde.
Het eigenaardige is dat Thomson en Tait niet merken hoe zij, om de theorie van de getijdenwrijving te onderbouwen, een theorie naar voren brengen die uitgaat van de stilzwijgende veronderstelling dat de aarde in zijn geheel een vast lichaam is en dus elke mogelijkheid van een vloed en dus ook van een getijdenwrijving uitsluit.